Given the slow but steady rise of quantum simulators, what are the hardware-efficient ways to implement chemical and physical models? How can we verify that we have implemented the right Hamiltonian? How can we efficiently characterize many-body states on such systems and measure them? Any quantum system is noisy, how can we find efficient ways to characterize and combat the noise?
Relevant Publications:
Many-body Chern number from statistical correlations of randomized measurements, Z-P. Cian, H. Dehghani, A. Elben, B. Vermersch, G. Zhu, M. Barkeshli, P. Zoller, and M. Hafezi , Phys. Rev. Lett., 126, 050501 (2021)
Hardware-efficient fermionic simulation with a cavity-QED system, G. Zhu, Y. Subasi, J. D. Whitfield, and M. Hafezi , npj Quantum Information, 4 (2018)
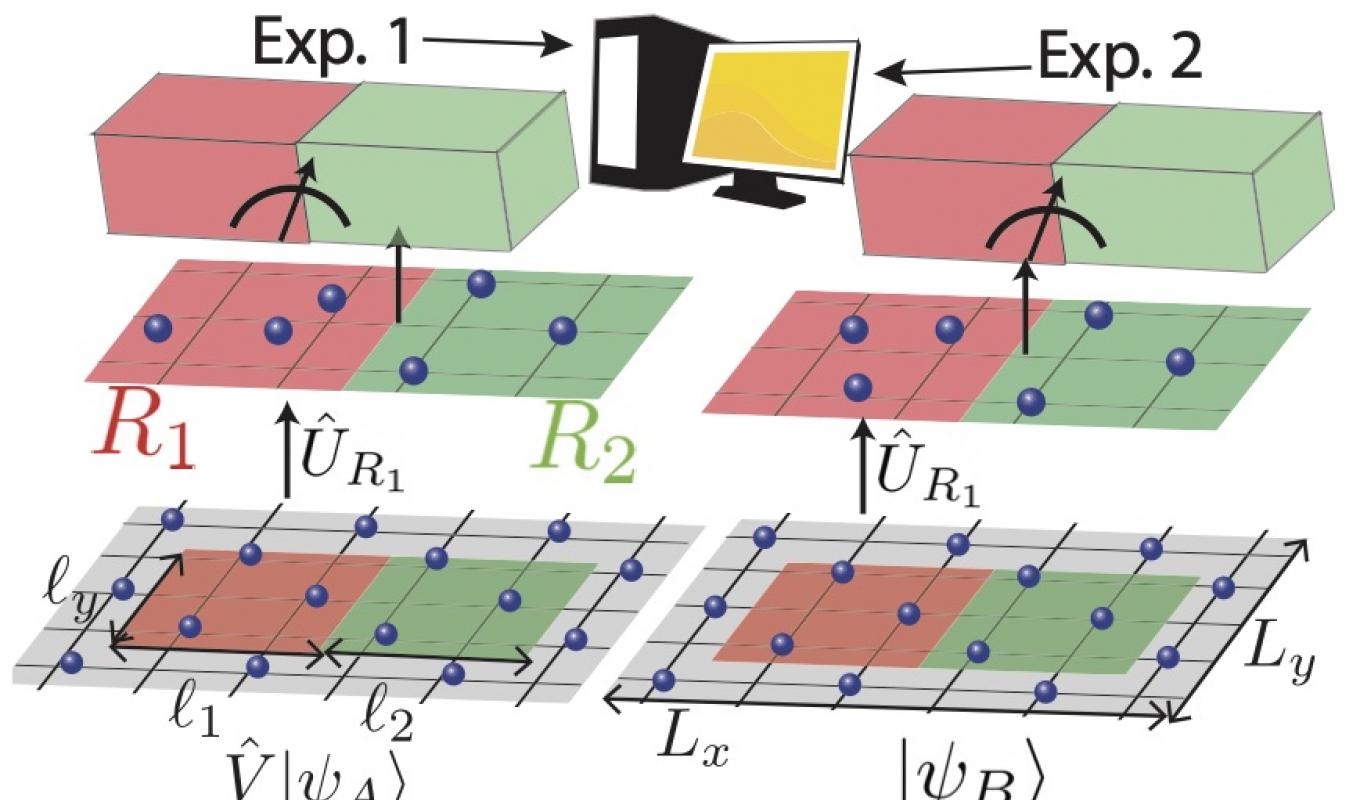
A Measurement Protocol for the Entanglement Spectrum of Cold Atoms, H. Pichler, G. Zhu, A. Seif, P. Zoller, and M. Hafezi , Phys. Rev. X 6, 041033 (2016) (2016)
Measurement of many-body chaos using a quantum clock, G. Zhu, M. Hafezi, and T. Grover , Phys. Rev. A 94, 062329 (2016) (2016)
Entanglement Entropy Scaling Transition under Competing Monitoring Protocols, M. Van Regemortel, Z-P. Cian, A. Seif, H. Dehghani, and M. Hafezi , Physical Review Letters, 126, 123604 (2021)
A Measurement Protocol for the Entanglement Spectrum of Cold Atoms, H. Pichler, G. Zhu, A. Seif, P. Zoller, and M. Hafezi , Phys. Rev. X 6, 041033 (2016) (2016)
Towards analog quantum simulations of lattice gauge theories with trapped ions, Z. Davoudi, M. Hafezi, C. Monroe, G. Pagano, A. Seif, and A. Shaw , Phys. Rev. Research, 2, 023015 (2020)
Meta Hamiltonian Learning, P. Bienias, A. Seif, and M. Hafezi , arXiv preprint arXiv:2104.04453 (2021)