Flat Bands
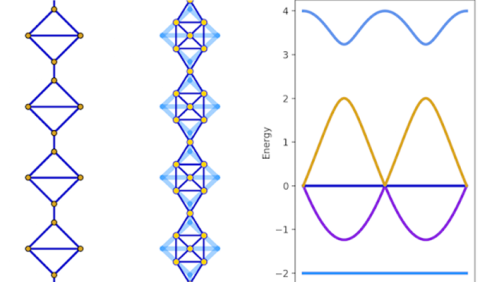
The one-dimensional nature of CPW lattice sites and their inherent deformability leads naturally to the implementation of line graphs with degenerate flat bands. Qubits coupled to these systems will mediate photon-photon interactions within the flat bands. They will also experience novel electromagnetic environments depending on their detuning with respect to the band structure. The resulting photonic bound states have new and controllable forms which give rise to new types of effective spin-spin interactions, including frustrated short-range antiferromagentism in the flat bands.
A. J. Kollár, M. Fitzpatrick, P. Sarnak, A.A. Houck, Line-Graph Lattices: Euclidean and Non-Euclidean Flat Bands and Implementations in Circuit QED, arXiv:1902.02794v1 (2019).
N. M. Sundaresan, R. Lundgren, G. Zhu, A. V. Gorshkov, and A. A. Houck, “Interacting Qubit-Photon Bound States with Superconducting Circuits,” Phys. Rev. X 9, 011021 (2019).
J. S. Douglas, H. Habibian, C.-L. Hung, A. V. Gorshkov, H. J. Kimble, and D. E. Chang, “Quantum many-body models with cold atoms coupled to photonic crystals,” Nat. Phys. 9, 326 (2012).
Hyperbolic Lattices

Curvature is fundamental aspect of general relativity, but negatively curved 2D hyperbolic manifolds cannot be isometrically imbedded in 3D Euclidean space. The natural deformability of CPW resonators allows for the implementation of table-top hyperbolic lattices with high curvature. Incorporating qubits into these devices, we can start to examine quantum mechanics in this unique environment.
A. J. Kollár, M. Fitzpatrick, P. Sarnak, A.A. Houck, Line-Graph Lattices: Euclidean and Non-Euclidean Flat Bands and Implementations in Circuit QED, arXiv:1902.02794v1 (2019).
A. J. Kollár, M. Fitzpatrick, A. A. Houck, Hyperbolic Lattices in Circuit Quantum Electrodynamics, Nature 571, 45-49 (2019), arXiv:1802.09549.
A. A. Houck, H. E. Türeci, and J. Koch, “On-chip quantum simulation with superconducting circuits,” Nat. Phys. 8, 292 (2012).
Interacting Chains
In the absence of fine tuning and many-body localization, large strongly-interacting closed systems are expected to self thermalize. Networks of qubits and resonators can be used to examine this behavior in the presence of drives and controllable dissipation set by qubit lifetimes and resonator coupling strengths.
M. Fitzpatick, N. M. Sundaresan, A. C. Y. Li, J. Koch, and A. A. Houck, “Observation of a Dissipative Phase Transition in a One-Dimensional Circuit QED Lattice,” Phys. Rev. X 7, 011016 (2017).
Raferty, J., D. Sadri, S. Schmidt, H. E. Türeci, A. A. Houck. Observation of a Dissipation-Induced Classical to Quantum Transition. Physical Review X 4, 031043 (2014).
A. A. Houck, H. E. Türeci, and J. Koch, “On-chip quantum simulation with superconducting circuits,” Nat. Phys. 8, 292 (2012).