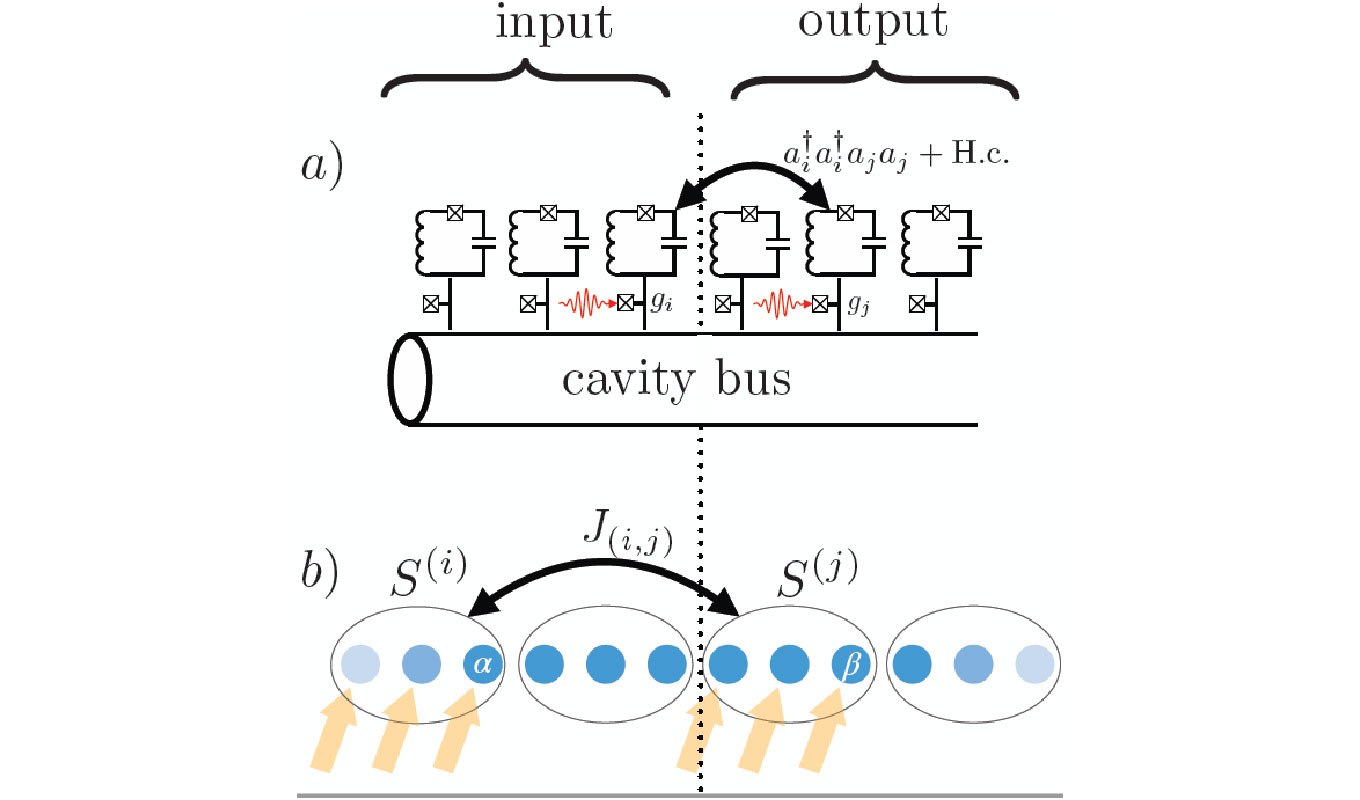
Recent progress on quantum random sampling protocols such as random circuit sampling and boson sampling demonstrate an advantage of quantum information processing. The main idea of various quantum random sampling protocols is to sample from the output distribution of random computations. Although such kinds of protocols are non-universal, the sampling task can be computationally difficult for classical computers. On one hand, random circuit sampling is designed for qubit systems that are intrinsically strongly interacting; on the other hand, boson sampling is designed for photonic devices that are non-interacting. The question arises: Is there an intermediately interacting regime where random sampling becomes intractable in a classical setting and becomes feasible on a quantum device? Because of the variety of quantum information processing platforms available that operate in the intermediately interacting regime, we found this question intriguing.
As you can read about in the paper linked below, we found that such an intermediately interacting regime could be feasibly utilized by a generalization of current boson sampling protocols. We introduce the concept of generalized bosons, whose local bosonic commutation [a,a^\dagger]=1 is replaced by an arbitrary single-mode operator that is diagonal in the generalized Fock basis. Then we prove the "boson sampling" for generalized bosons produces similar hardness results as would be expected using classical methods. Finally, we provide two concrete examples of generalized boson sampling protocols in ion-trap and circuit-QED platforms.
Watch the video here: https://www.youtube.com/watch?v=ysas6DzAogI
Read the full article here: https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.4.043096#:~:text=Examples%20of%20generalized%20bosons%20include,of%20sampling%20directly%20carry%20over.