
Colors representing new phases of matter produce a zoo of fractal plots that look like butterfly wings. (Credit: Yuxuan Zhang /JQI)
Matter—all the stuff we see around us—can be classified into familiar phases: our chairs are solid, our coffee is liquid, and the oxygen we breathe is a gas. This grouping obscures the nitty gritty details of what each molecule or atom is up to and reduces all that complexity down to a few main features that are most salient in our everyday lives.
But those are not the only properties of matter that matter. Focusing on solids, physicists have found that they can group things according to symmetries. For example, atoms in solids arrange themselves into repeating patterns, forming crystals that can be grouped according to whether they look the same left and right, up and down, rotated about, and more. In the 1980s, physicists discovered a new paradigm: In addition to symmetries, solids can be classified using topology—a field of math that does for geometrical shapes the same kind of thing that symmetries do for crystalline solids. All the shapes without holes (a ball, a pizza) are in the same topological “phase,” while those with one hole (a donut, a coffee mug) are in a different “phase,” and so on with each new hole.
Within physics, topology doesn’t usually refer to the shape a piece of metal is cut into. Rather, the topology of how electrons are arranged inside a crystal provides information about the material’s electrical conductance and other properties. Now, theorists at the Joint Quantum Institute have found that these same crystals hide a richer set of topological phases than previously thought. In two separate works, they revealed a host of possible topological phases that become apparent when two different kinds of defects develop in crystals, or when they study the twirling properties of the electronic arrangement. They published their findings in the journal Physical Review X on July 14, 2023 and in the journal Physical Review Letters in Dec. 2022.
“Condensed matter physics is about understanding all the properties of phases of matter,” says Naren Manjunath, a graduate student at JQI and an author on both results. “I think that our work is really expanding our understanding of how to define new topological properties and how to characterize phases of matter better.”
Topology was first recognized as an important matter-classification tool after the discovery of the quantum Hall effect in the 1980s. When thin sheets of certain materials are pierced by a strong magnetic field, the electrons inside the materials spin around in circles—the larger the magnetic field the tighter their turns. Once the circles get small enough, quantum mechanics kicks in and dictates that the size of the circles can only have certain discrete values (the “quantum” in the quantum Hall effect). As the magnetic field is increased, nothing changes for a while—there is a plateau. Then, when the field gets large enough, electrons suddenly hop into a tighter orbit—an abrupt, step-wise change.
This jump from one radius of a spinning orbit to another can be thought of as a change in the topological phase—the geometry of the electron motion in the material switches. This sudden hopping is extremely precise, and it results in abrupt jumps in the electrical conductivity of the metal sheet, making the topological phase easy to measure experimentally.
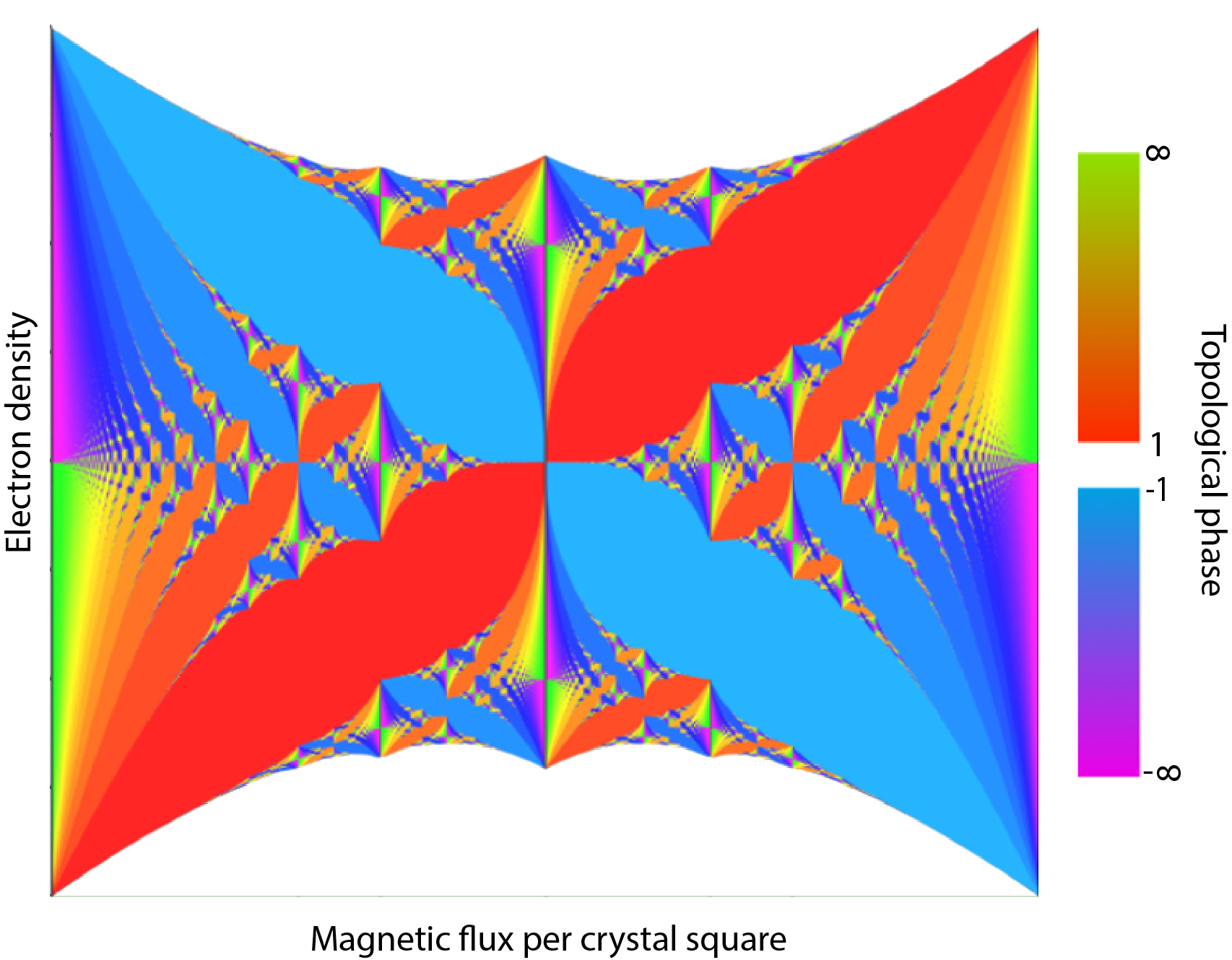
Even more interesting things would happen if the magnetic field in the quantum Hall effect was cranked up so high that the electron orbitals became about as small as the atomic spacing in the crystal. There, electrons arrange themselves into different topological phases that depend on how many electrons were around in the first place and the magnetic field piercing each little bit of the crystal. A color-coded plot of conductivity as it depends on the electron density and the magnetic field appears as a winged butterfly, called the Hofstadter butterfly after the theoretical physicist that first studied this model.
“We're furthering this program of trying to find all possible quantized numbers that could be associated with phases of matter,” says JQI Fellow Maissam Barkeshli, who is also an associate professor of physics at UMD and a principal investigator on the work. “And this is a long-term program and we made a lot of progress on it recently.”
Manjunath, Barkeshli, and their collaborators found that there may be more intricate details hiding in the Hofstadter butterfly’s wings than previously thought. Some spots on the butterfly might have the same color, and therefore the same topological phase in the original treatment, and yet behave differently from each other in important ways.
These extra distinguishing features are always present, but they become most obvious when the crystal develops defects—little mistakes in its otherwise perfectly regular pattern. The way electrons behave around this defect would differ depending on the underlying topological phase. And different defects can help uncover different kinds of phases.
The team first studied an imperfection called a disclination, which occurs when a piece of the crystal is taken out and the remaining atoms are stitched back together, as seen in the diagram below. The researchers found that electric charge tends to cluster around this defect. And how much charge pops up at the defect depends on a new quantity, which the team called the shift. Much like the size of electron orbits in the quantum Hall effect, the shift is quantized: It can only be an integer or a half-integer. A different value of the shift corresponds to a different phase of matter. The electric charge appearing at a disclination would be a multiple of this shift, which, weirdly enough, could even be a fraction of a single electron’s charge. They published the results of their theoretical investigation in the journal Physical Review Letters in December 2022.
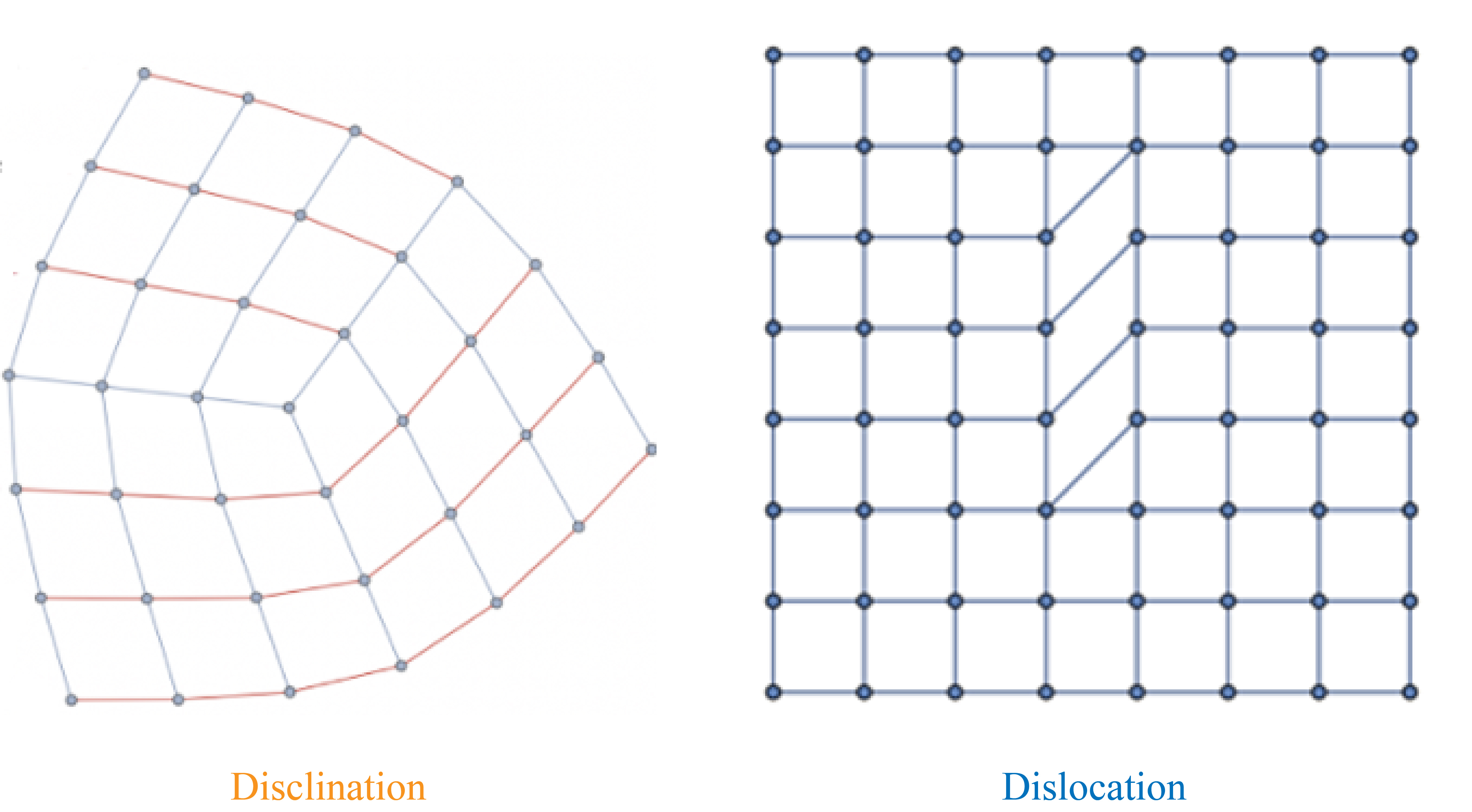
After disclinations, the team focused their attention on another kind of imperfection called a dislocation. Unlike a disclination, no atoms are missing in a dislocation. Instead, the connections between atoms in a crystal are rewired in a different order. Instead of being connected to its closest neighbor, one or more of the atoms bonds with the next atom over, creating a skewed ladder of links.
Dislocations turned out to have another quantized quantity associated with them, this time named a quantized polarization. Inside a perfectly regular crystal, every tiny square of the lattice may hide a bit of charge polarization—one side becomes somewhat positively charged while the other side becomes a bit negatively charged. This polarization is hard to spot. If a dislocation is introduced, however, the researchers found that one side of this polarized charge gets trapped in the defect, revealing the extent of the polarization. Exactly how polarized they would become depended directly on the underlying quantized polarization. The team published this result in the journal Physical Review X.
Each of these quantities—the shift and the quantized polarization—has consequences even without any defects. These consequences have to do with the way the electrons tend to twist around different points inside the crystal lattice. But these twists are tricky to find experimentally, while crystal defects offer a tangible way of measuring and observing these new quantities by trapping charges in their vicinity.
New butterflies, cousins of the original Hofstadter butterfly, pop up thanks to the shift and quantized polarization. Both can be plotted as a function of electron density and magnetic field and exhibit the same winged, fractal butterfly-like structure. The researchers believe more such quantities and their associated phases remain to be uncovered, associated with yet more defects. “Eventually we expect we will have a large number of beautiful colored butterfly figures,” Barkeshli says, “one for each of these topological properties.”
For now, testing these predictions experimentally seems just out of reach. The Hofstadter model requires such large magnetic fields that it cannot be realized in regular materials. Instead, people have resorted to simulating this model with synthetic lattices of atoms or photons, or in layered graphene structures. These synthetic lattices are not quite large enough to measure the charge distributions required, but with some engineering advances, they might be up to the task in the coming years. It may also be possible to create these lattices using small, noisy quantum computers that have already been built, or topological photonic systems.
“We only considered the Hofstadter model,” says Manjunath, “but you could measure the same thing for more exotic phases of matter. And some of those phases might actually have some applications in the very distant future.”
Story by Dina Genkina
In addition to Manjunath and Barkeshli, authors on the publications included UMD graduate students Yuxuan Zhang and Gautam Nambiar.